二叉堆

什么是二叉堆

只要满足下面的结构性质和堆序性质的，就是二叉堆

结构性质

二叉堆是一颗被完全填满的二叉树，有可能的例外是在底层，底层上的元素从左到右填入。这样的树称为完全二叉树。

完全二叉树

容易证明，一颗高为 h 的完全二叉树有$2^h$到$2^{h+1} - 1$个节点。这意味着，完全二叉树的高是$\lfloor logN \rfloor$，显然它是$O(logN)$

一个重要的观察发现，因为完全二叉树这么有规律，所以它可以用一个数组表示

完全二叉树的数组实现

该数组索引为 0 的位置是空的，元素是从索引为 1 的位置开始放入的。这样的话，对于数组中的任意位置$i$上的元素，其左儿子在位置$2i$上，右儿子在左儿子后的单元$2i+1$中，它的父亲则在位置$\lfloor i/2 \rfloor$上。

堆序性质

使操作被快速执行的性质是堆序性质。由于我们想要能够快速地找出最小/大元，因此最小/大元应该在根上。如果我们考虑任意子树也应该是一个堆，那么任意节点就应该小/大于它的所有后裔。

最小/大堆

二叉堆分为最小堆和最大堆

最小堆：在最小堆中，对于每一个节点 X，X 的父亲中的关键字小于（或等于）X 中的关键字，根节点除外（它没有父亲）
最大堆：在最大堆中，对于每一个节点 X，X 的父亲中的关键字大于（或等于）X 中的关键字，根节点除外（它没有父亲）

二叉堆的操作

下面的操作，均以最小堆为例

insert

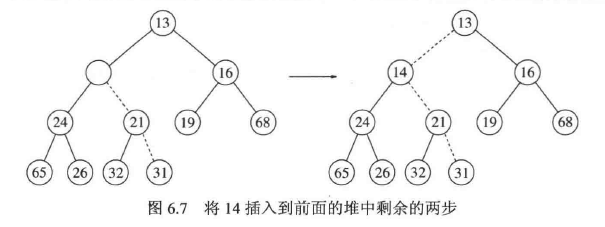
为了将一个元素 X 插入到堆中，我们必须在下一个可用位置创建一个空穴，否则该堆将不是完全二叉树了。如果 X 可以放在该空穴中而并不破坏堆的序，那么插入完成。否则，我们把空穴的父节点上的元素移入该空穴中，这样，空穴就朝着根的方向上冒一步。继续该过程直到 X 能被放入空穴中位置。这种一般的策略叫作上滤。

时间复杂度（最坏）：$O(logN)$

insert1
insert2

deleteMin

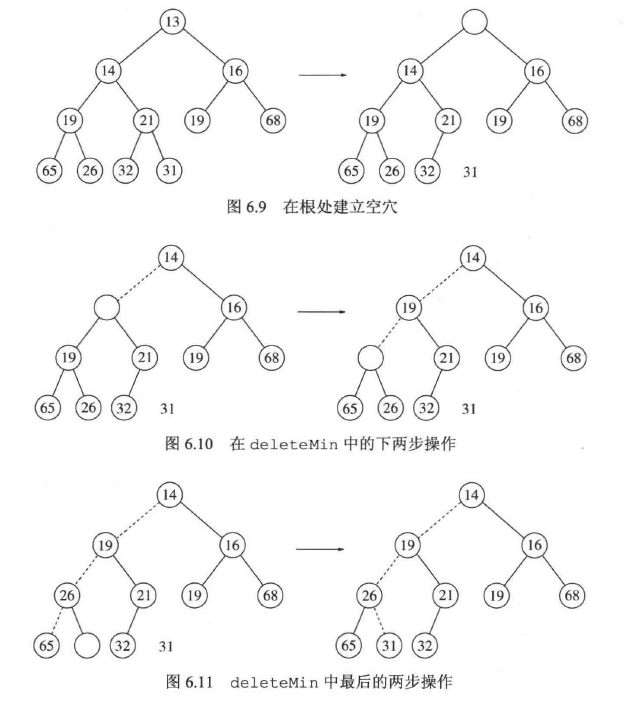
当删除一个最小元时，要在根节点建立一个空穴。由于现在的堆少了一个元素，因此堆中最后一个元素 X 必须移动到该堆的某个地方。如果 X 可以被放到空穴中，那么 deleteMin 就完成。否则我们将空穴的两个儿子中较小者移入空穴，这样就把空穴向下推了一层。重复该步骤直到 X 可以被放入空穴中。因此，我们的做法是将 X 置入沿着从根节点开始包含最小儿子的一条路径上的一个正确的位置。这种一般的策略叫作下滤。

时间复杂度（最坏）：$O(logN)$

deleteMin

decreaseKey

decreaseKey(p, △) 操作降低在位置 p 处的项的值，降值的幅度为正的量 △。由于这可能破坏堆序性质，因此必须通过上滤堆堆进行调整。

increaseKey

increaseKey(p, △) 操作增加在位置 p 处的项的值，增值的幅度为正的量 △。这可以用下滤来完成。

remove

remove(p) 操作删除堆中位置 p 上的节点。该操作通过首先执行 decreaseKey(p, ∞) 然后再执行 deleteMin 来完成。

buildHeap

有时二叉堆是由一些项的一个初始集合构造而得的，当然可以使用连续的 insert 操作来完成堆的构建，但是这样的话最坏情况下的时间复杂度为 $O(NlogN)$，这并不是最优的方案。

最优方案步骤：

将这些项构成的集合直接转换为一个无序的完全二叉树
从完全二叉树的最后一个非叶子节点开始往前遍历，依次进行下滤策略

时间复杂度（最坏）：$O(N)$

let list = [90, 84, 83, 88, 87, 61, 50, 70, 60, 80];

function buildHeap(array) {
  let heap = [];
  heap.size = array.length;
  for (let i = 0; i < array.length; i++) {
    heap[i + 1] = array[i];
  }

  let currentIndex = Math.floor(heap.size / 2);
  while (currentIndex > 0) {
    percolateDown(heap, currentIndex);
    currentIndex--;
  }

  return heap;
}

function percolateDown(heap, currentIndex) {
  let leftSonIndex = 2 * currentIndex,
    rightSonIndex = 2 * currentIndex + 1,
    minValueIndex = currentIndex;

  if (leftSonIndex <= heap.size && heap[leftSonIndex] < heap[currentIndex]) {
    minValueIndex = leftSonIndex;
  }

  if (rightSonIndex <= heap.size && heap[rightSonIndex] < heap[minValueIndex]) {
    minValueIndex = rightSonIndex;
  }

  if (currentIndex !== minValueIndex) {
    [heap[currentIndex], heap[minValueIndex]] = [
      heap[minValueIndex],
      heap[currentIndex],
    ];
    percolateDown(heap, minValueIndex);
  }
}

console.log(buildHeap(list));

$d$堆

$d$ 堆是二叉堆的简单推广，它恰像一个二叉树，只是所有的节点都有 $d$ 个儿子（因此，二叉堆是 2 堆）。

$d$ 堆要比二叉堆浅得多，它将 insert 操作的运行时间改进为 $O(log_dN)$。然而，对于大的 $d$，deleteMin 操作费时得多，因为虽然树是浅了，但是 $d$ 个儿子中的最小者是必须要找出的，如果使用标准的算法，这会花费 $d-1$ 次比较，于是将操作的用时提高到 $O(dlog_dN)$。如果 $d$ 是常数，那么当然两者的运行时间都是 $O(logN)$。最后，有证据显示，在实践中 4 堆可以胜过二叉堆。

左式堆

左式堆像二叉堆那样也具有结构性和有序性。事实上，和所有使用的堆一样，左式堆具有相同的堆序性质。左式堆与二叉堆的区别主要体现在结构性上。

结构性质

我们把任意节点 X 的零路径长npl(X)定义为从 X 到一个不具有两个儿子的节点的最短路径长。因此，具有 0 或 1 个儿子的节点的npl = 0，而空节点的npl = -1。

任意节点的零路径长比它的诸儿子节点的零路径长的最小值多 1。这个结论也适用少于两个儿子的节点。

左式堆的结构性质是：对于每一个节点 X，左儿子的零路径长至少与右儿子的零路径长一样。对于堆中的每一个节点 X，左儿子的零路径长大于等于右儿子的零路径长
《数据结构与算法分析》中有证明，在右路径上有$r$个节点的左式堆必然至少有$2^r-1$个节点

左式堆操作

merge

这里我要介绍的是递归进行合并的方法。当要合并两个堆时，如果有一个是空的，则直接返回另一个堆。否则，为了合并这两个堆，可比较它们的根。首先，递归地将具有较大的根植的堆与具有较小的根植的堆的右子堆合并，然后判断左子堆和新的右子堆的零路径长，如果不满足左式堆的结构性，那么交换左子堆与右子堆的位置。

insert

insert 可以看作是 merge 的一种特殊情况，就是把插入看作是单节点堆与一个更大的堆的 merge。

deleteMin

deleteMin 也可以看作是 merge 的一种特殊情况，首先将根节点移除，然后对两个儿子进行 merge 操作。