排序算法总结

发表于 | 更新于 | 分类于

基本概念

排序算法可以分为以下两种类型：

  • 比较类非线性时间排序：通过比较来决定元素间的相对次序，其时间复杂度不能突破$O(nlogn)$
  • 非比较类线性时间排序：不通过比较来决定元素间的相对次序，其时间复杂度最低可以为$O(n)$
  • 稳定性：如果排序前后两个相等元素的相对次序不变，则算法稳定；反之算法不稳定

冒泡排序

  • 实现步骤（从小到大排序）：
    1. 从最前面的两个元素开始，不断对相邻元素进行比较，根据情况决定是否交换相邻元素的位置，直到最后。这会将最大的元素“冒泡”到元素列的末尾位置。
    2. 步骤 1 需要被重复执行 n-1 次。但是每一趟排序时，不是全部元素都需要进行比较的。例如，对于第 m 趟排序，此时元素列最后面的 m 个元素是已经完成排序了的，所以不需要对它们进行重复的比较。
  • 最坏时间复杂度：$O(n^2)$
  • 平均时间复杂度：$O(n^2)$
  • 最好时间复杂度：$O(n)$
  • 空间复杂度：$O(1)$
  • 稳定性：稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
let list = [84, 83, 88, 87, 61, 50, 70, 60, 80];

function bubbleSort(array) {
  console.log(array.join('   '));

  let len = array.length;
  for (let i = 0; i < len - 1; i++) {
    for (let j = 0; j < len - 1 - i; j++) {
      if (array[j] > array[j + 1]) {
        [array[j], array[j + 1]] = [array[j + 1], array[j]];
      }
    }
    console.log(array.join('   '));
  }
}

bubbleSort(list);

冒泡排序

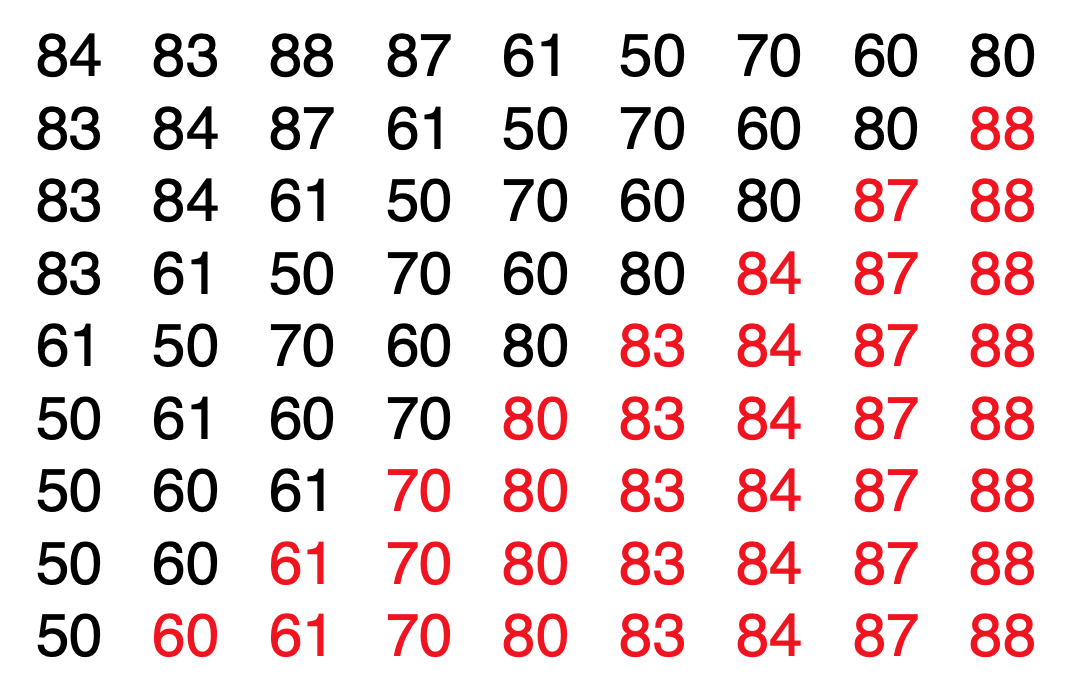
选择排序

  • 实现步骤（从小到大排序）：
    1. 共需要进行 n-1 次循环。每次循环都会选定一个起点元素，例如，第一次循环是以第一个元素为起点。第 m 次循环是以第 m 个元素为起点。
    2. 在每次循环中，找出本次循环中从起点元素开始到最后一个元素为止最小的元素，如果这个元素正是起点元素则什么都不做，否则交换起点元素与该最小元素的位置。
  • 最坏时间复杂度：$O(n^2)$
  • 平均时间复杂度：$O(n^2)$
  • 最好时间复杂度：$O(n^2)$
  • 空间复杂度：$O(1)$
  • 稳定性：不稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
let list = [84, 83, 88, 87, 61, 50, 70, 60, 80];

function selectionSort(array) {
  console.log(array.join('   '));

  let len = array.length;
  let mixIndex;
  for (let i = 0; i < len - 1; i++) {
    mixIndex = i;
    for (let j = i + 1; j < len; j++) {
      if (array[j] < array[mixIndex]) {
        mixIndex = j;
      }
    }
    [array[mixIndex], array[i]] = [array[i], array[mixIndex]];
    console.log(array.join('   '));
  }
}

selectionSort(list);

选择排序

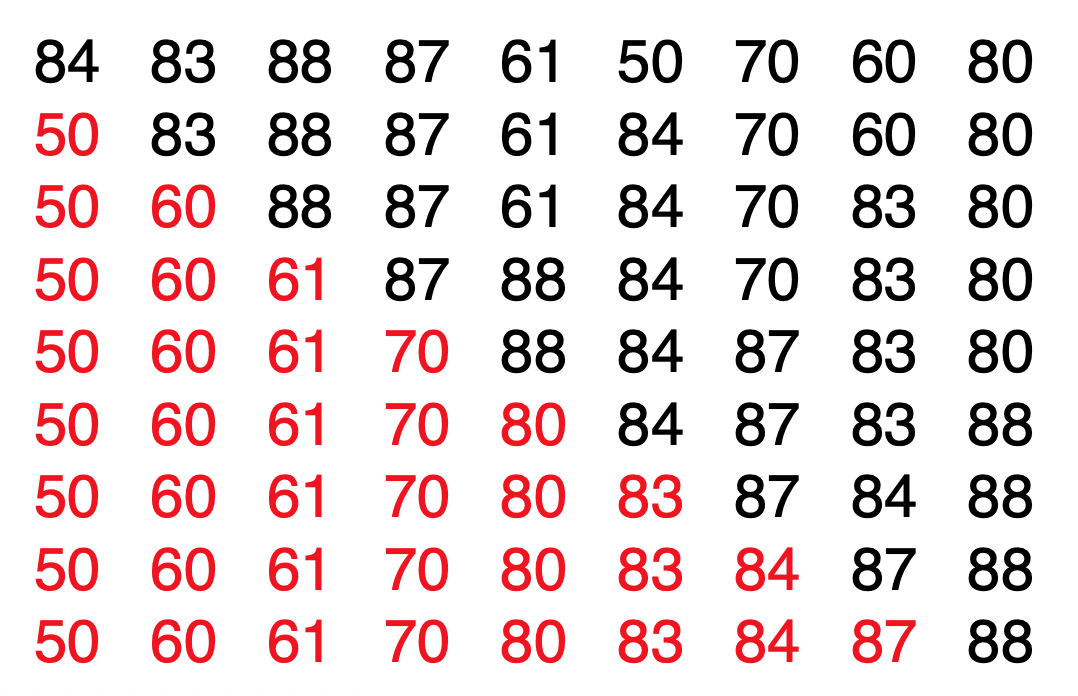
插入排序

  • 实现步骤（从小到大排序）：
    1. 共需要进行 n-1 次循环。每次循环都会选定一个待插入元素，例如，第一次循环是以第二个元素为待插入元素。第 m 次循环是以第 m+1 个元素为待插入元素。
    2. 在每次循环中，不断将待插入元素与处于它前方的元素进行比较，找出适合它的位置并插入。
  • 最坏时间复杂度：$O(n^2)$
  • 平均时间复杂度：$O(n^2)$
  • 最好时间复杂度：$O(n)$
  • 空间复杂度：$O(1)$
  • 稳定性：稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
let list = [84, 83, 88, 87, 61, 50, 70, 60, 80];

function insertionSort(array) {
  console.log(array.join('   '));

  let len = array.length;
  for (let i = 1; i < len; i++) {
    let unsortValue = array[i];
    let currentIndex = i - 1;
    while (currentIndex >= 0 && array[currentIndex] > unsortValue) {
      array[currentIndex + 1] = array[currentIndex];
      currentIndex--;
    }
    array[currentIndex + 1] = unsortValue;
    console.log(array.join('   '));
  }
}

insertionSort(list);

插入排序

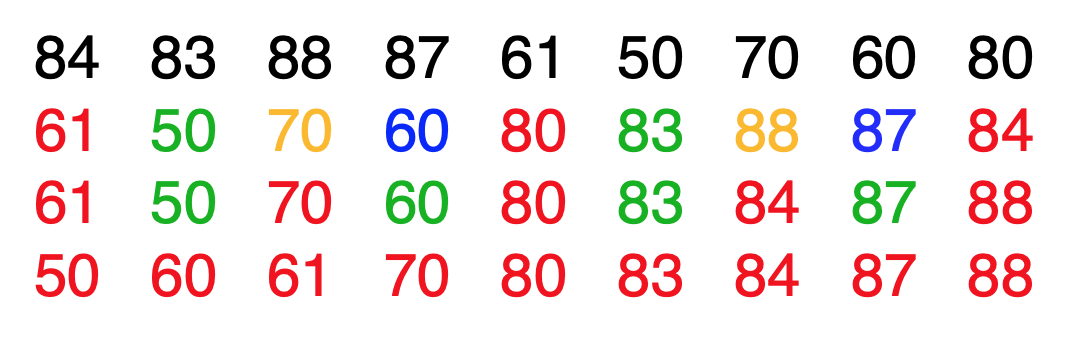
希尔排序

  • 实现步骤（从小到大排序）：
    1. 按照步长n/2 => n/4 => ··· => 1进行循环。每次循环中根据步长对元素列进行分组，然后对这些分组执行插入排序。
  • 最坏时间复杂度：$O(n^2)$
  • 平均时间复杂度：$O(n^{1.3})$
  • 最好时间复杂度：$O(n)$
  • 空间复杂度：$O(1)$
  • 稳定性：不稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
let list = [84, 83, 88, 87, 61, 50, 70, 60, 80];

function shellSort(array) {
  console.log(array.join('   '));

  let len = array.length;
  for (let gap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
    // 内部为插入排序
    for (let i = gap; i < len; i++) {
      let unsortValue = array[i];
      let currentIndex = i - gap;
      while (currentIndex >= 0 && array[currentIndex] > unsortValue) {
        array[currentIndex + gap] = array[currentIndex];
        currentIndex = currentIndex - gap;
      }
      array[currentIndex + gap] = unsortValue;
    }
    console.log(array.join('   '));
  }
}

shellSort(list);

希尔排序

归并排序

  • 实现步骤（从小到大排序）：
    1. 不断地将元素列分成两个部分，然后对这两个部分递归执行归并排序。
    2. 当元素列只有 1 个元素时，停止递归。
    3. 对于被划分的两个部分，需要按照顺序将它们合并为一个整体。
  • 最坏时间复杂度：$O(nlogn)$
  • 平均时间复杂度：$O(nlogn)$
  • 最好时间复杂度：$O(nlogn)$
  • 空间复杂度：$O(n)$
  • 稳定性：稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
let list = [84, 83, 88, 87, 61, 50, 70, 60, 80];

function mergeSort(array) {
  let len = array.length;

  if (len < 2) {
    return array;
  } else {
    let middle = Math.floor(len / 2),
      left = array.slice(0, middle),
      right = array.slice(middle);

    return merge(mergeSort(left), mergeSort(right));
  }
}

function merge(left, right) {
  let result = [];

  while (left.length > 0 && right.length > 0) {
    if (left[0] <= right[0]) {
      result.push(left.shift());
    } else {
      result.push(right.shift());
    }
  }

  while (left.length) {
    result.push(left.shift());
  }

  while (right.length) {
    result.push(right.shift());
  }

  return result;
}

mergeSort(list);

快速排序

  • 实现步骤（从小到大排序）：
    1. 通过三数中值分割法，从元素列中选出最左侧，中间和最右侧的三个元素，并排序。
    2. 从步骤 1 中排序后的三个元素中选择中间元素作为枢纽元素，并交换枢纽元素和元素列倒数第二个元素的位置。
    3. 选择i = left + 1, j = right - 2。
    4. 不断执行i++操作，直到i所处元素大于等于枢纽元素为止。
    5. 不断执行j--操作，直到j所处元素小于等于枢纽元素为止。
    6. 如果i < j，那么交换这两个位置上的元素，然后重复执行步骤 4、5。
    7. 如果i >= j，那么此刻位置i上的元素一定是大于等于枢纽元素的，此时交换位置i上的元素和枢纽元素的位置。交换之后，枢纽元素左侧的元素均小于等于它，而它右侧的元素均大于等于它。
    8. 不断对被枢纽元素分割开来的两个子元素列执行步骤 1 至步骤 7，直到排序完成。
  • 最坏时间复杂度：$O(n^2)$
  • 平均时间复杂度：$O(nlgn)$
  • 最好时间复杂度：$O(nlgn)$
  • 空间复杂度：$O(lgn)$ 至 $O(n)$ 之间
  • 稳定性：不稳定
  • 需要注意array[i]=array[j]=pivot的情况，不要陷入死循环。
  • 为什么当所遇元素与枢纽元素相等时，也要让i和j停下来，并交换位置？
    这样可以确保被枢纽元素分割开来的两部分尽量均衡，减少插入排序算法总的时间复杂度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
let list = [84, 83, 88, 87, 61, 50, 70, 60, 80];

function quickSort(array, left, right) {
  var left = typeof left !== 'number' ? 0 : left,
    right = typeof right !== 'number' ? array.length - 1 : right;

  if (left === right) {
    return;
  }

  if (left + 1 === right) {
    if (array[left] <= array[right]) {
      return;
    } else {
      [array[left], array[right]] = [array[right], array[left]];
      return;
    }
  }

  let pivot = median3(array, left, right),
    i = left + 1,
    j = right - 2;

  while (i < j) {
    while (array[i] < pivot) {
      i++;
    }
    while (pivot < array[j]) {
      j--;
    }
    if (i < j) {
      if (array[i] === array[j]) {
        i++;
      } else {
        [array[i], array[j]] = [array[j], array[i]];
      }
    }
    if (i >= j) {
      break;
    }
  }

  [array[i], array[right - 1]] = [array[right - 1], array[i]];

  quickSort(array, left, i - 1);
  quickSort(array, i + 1, right);
}

function median3(array, left, right) {
  let center = Math.floor((left + right) / 2);

  if (array[center] < array[left]) {
    [array[left], array[center]] = [array[center], array[left]];
  }
  if (array[right] < array[left]) {
    [array[left], array[right]] = [array[right], array[left]];
  }
  if (array[right] < array[center]) {
    [array[center], array[right]] = [array[right], array[center]];
  }

  [array[center], array[right - 1]] = [array[right - 1], array[center]];

  return array[right - 1];
}

quickSort(list);

堆排序

  • 实现步骤（从小到大排序）：
    1. 首先将元素列转换为最大堆形式的数组。
    2. 数组中的最大元素总在 A[1] 中，把它与 A[heap.size] 进行互换，同时从堆中去掉最后一个结点（这一操作可以通过减少 heap.size 来实现）。
    3. 步骤 2 之后，最大堆的剩余结点中，原来根的孩子结点仍然是最大堆，而新的根节点可能会违背最大堆的性质。为了维护最大堆的性质，我们要做的就是通过下滤操作使其符合最大堆的性质。
    4. 重复步骤 2、3，直到 heap.size = 1。
  • 最坏时间复杂度：$O(nlgn)$
  • 平均时间复杂度：$O(nlgn)$
  • 最好时间复杂度：$O(nlgn)$
  • 空间复杂度：$O(1)$
  • 稳定性：不稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
let list = [90, 84, 83, 88, 87, 61, 50, 70, 60, 80];

function heapSort(array) {
  let heap = buildHeap(array);

  for (let i = heap.size; i > 1; i--) {
    [heap[i], heap[1]] = [heap[1], heap[i]];
    heap.size--;
    percolateDown(heap, 1);
  }

  return heap.slice(1);
}

function buildHeap(array) {
  let heap = [];
  heap.size = array.length;
  for (let i = 0; i < array.length; i++) {
    heap[i + 1] = array[i];
  }

  let currentIndex = Math.floor(heap.size / 2);
  while (currentIndex > 0) {
    percolateDown(heap, currentIndex);
    currentIndex--;
  }

  return heap;
}

function percolateDown(heap, currentIndex) {
  let leftSonIndex = 2 * currentIndex,
    rightSonIndex = 2 * currentIndex + 1,
    maxValueIndex = currentIndex;

  if (leftSonIndex <= heap.size && heap[leftSonIndex] > heap[currentIndex]) {
    maxValueIndex = leftSonIndex;
  }

  if (rightSonIndex <= heap.size && heap[rightSonIndex] > heap[maxValueIndex]) {
    maxValueIndex = rightSonIndex;
  }

  if (currentIndex !== maxValueIndex) {
    [heap[currentIndex], heap[maxValueIndex]] = [
      heap[maxValueIndex],
      heap[currentIndex],
    ];
    percolateDown(heap, maxValueIndex);
  }
}

console.log(heapSort(list)); // [ 50, 60, 61, 70, 80, 83, 84, 87, 88, 90 ]

计数排序

  • 实现步骤（从小到大排序）：
    1. 假设元素列中的元素均处于 $[0, k]$ 区间内，$k$ 为某个整数。
    2. 准备一个长度为 $k+1$ 的数组 temp，索引为 $i$ 处记录着元素列中值为 $i$ 的元素的个数。
    3. 调整数组 temp，使得索引为 $i$ 处记录着元素列中值小于等于 $i$ 的元素的个数。
    4. 准备一个长度为 $n$ 的数组 res 用于存储排序后的元素列，然后从后至前的迭代待排序的元素列，根据 temp 确定每次迭代的元素应该处于哪个位置，同时对 temp 进行适当的修改。
  • 时间复杂度：$\Theta(n+k)$
  • 空间复杂度：$O(n+k)$
  • 稳定性：稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
let list = [2, 5, 3, 0, 2, 3, 0, 3];

function countingSort(array) {
  let temp = [];

  array.forEach((item) => {
    if (typeof temp[item] === 'number') {
      temp[item] = temp[item] + 1;
    } else {
      temp[item] = 1;
    }
  });

  for (let i = 0; i < temp.length; i++) {
    let cur = typeof temp[i] === 'number' ? temp[i] : 0;
    if (i === 0) {
      temp[i] = cur;
    } else {
      temp[i] = cur + temp[i - 1];
    }
  }

  let res = [];
  for (let i = array.length - 1; i >= 0; i--) {
    let value = array[i];
    res[temp[value] - 1] = value;
    temp[value] = temp[value] - 1;
  }
  return res;
}

console.log(countingSort(list)); // [ 0, 0, 2, 2, 3, 3, 3, 5 ]

桶排序

  • 实现步骤（从小到大排序）：
    1. 假设元素列中的元素均处于 $[0, 1）$ 区间内。
    2. 准备一个长度为 10 的数组 temp。
    3. 假设元素的值为 $x$，则将它放入 temp 数组索引为 $\lfloor 10x \rfloor$ 的位置。
    4. 对数组 temp 下的每个“桶”进行排序，然后将排序后的“桶”拼接在一起。
  • 时间复杂度：需要考虑每个桶内排序所消耗的时间
  • 空间复杂度：$O(n+k)$
  • 稳定性：稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
let list = [0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 0.68];

function bucketSort(array) {
  let temp = Array.from(Array(10), () => []);

  array.forEach((item) => {
    let index = Math.floor(item * 10);
    temp[index].push(item);
  });

  temp = temp.map((item) => {
    if (temp.length > 0) {
      insertionSort(item);
    }
    return item;
  });

  return [].concat(...temp);
}

function insertionSort(array) {
  let len = array.length;
  for (let i = 1; i < len; i++) {
    let unsortValue = array[i];
    let currentIndex = i - 1;
    while (currentIndex >= 0 && array[currentIndex] > unsortValue) {
      array[currentIndex + 1] = array[currentIndex];
      currentIndex--;
    }
    array[currentIndex + 1] = unsortValue;
  }
}

console.log(bucketSort(list)); // [ 0.12, 0.17, 0.21, 0.23, 0.26, 0.39, 0.68, 0.72, 0.78, 0.94 ]

基数排序

  • 实现步骤（从小到大排序）：
    1. 从最低有效位开始，依次根据当前位的关键字对元素列使用稳定排序算法进行排序。
  • 时间复杂度：
    1. 给定 $n$ 个 $d$ 位数，其中每一个数位有 $k$ 个可能的取值。如果使用的稳定排序方法耗时 $\Theta(n+k)$，那么它就可以在 $\Theta(d(n+k))$ 时间内将这些数排好序。
    2. 给定一个 $b$ 位数和任何正整数 $r \leq b$，如果使用稳定排序算法对数据取值区间为 $[0, k]$ 的输入进行排序耗时 $\Theta(n+k)$，那么它就可以在 $\Theta((b/r)(n+2^r))$ 时间内将这些数排好序。
  • 空间复杂度：由过程中使用的稳定排序算法决定
  • 稳定性：稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
let list = [329, 457, 657, 839, 436, 720, 355, 11, 20, 4];

function radixSort(array, d) {
  array = array.map((item) => {
    let str = String(item),
      len = str.length;

    return '0'.repeat(d - len) + str;
  });

  for (let i = d - 1; i >= 0; i--) {
    let temp = [];

    array.forEach((item) => {
      if (typeof temp[item[i]] === 'number') {
        temp[item[i]] = temp[item[i]] + 1;
      } else {
        temp[item[i]] = 1;
      }
    });

    for (let j = 0; j < temp.length; j++) {
      let cur = typeof temp[j] === 'number' ? temp[j] : 0;
      if (j === 0) {
        temp[j] = cur;
      } else {
        temp[j] = cur + temp[j - 1];
      }
    }

    let res = [];
    for (let j = array.length - 1; j >= 0; j--) {
      let value = array[j],
        singleValue = array[j][i];
      res[temp[singleValue] - 1] = value;
      temp[singleValue] = temp[singleValue] - 1;
    }
    array = res;
  }

  return array.map((item) => parseInt(item));
}

console.log(radixSort(list, 3)); // [ 4, 11, 20, 329, 355, 436, 457, 657, 720, 839 ]


感谢您的阅读，如果发现文章中有错误或漏洞，请批评指正。
邮箱：aadonkeyz@gmail.com

0%