算法的分析

渐近记号

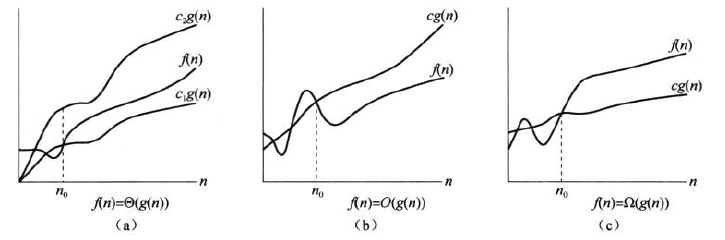
• 如果存在正常数 $c$ 和 $n_0$，使得当 $n \geq n_0$ 时，$0 \leq f(n) \leq cg(n)$， 则记为 $f(n) = O(g(n))$。
• 如果存在正常数 $c$ 和 $n_0$，使得当 $n \geq n_0$ 时，$0 \leq cg(n) \leq f(n)$， 则记为 $f(n) = \Omega(g(n))$。
• 如果存在正常数 $c_1$、$c_2$ 和 $n_0$，使得当 $n \geq n_0$ 时，$0 \leq c_1g(n) \leq f(n) \leq c_2g(n)$，则记为 $f(n) = \Theta(g(n))$。
• $f(n) = O(g(n)) 且 f(n) = \Omega(g(n))$ $\iff$ $f(n) = \Theta(g(n))$。

---

• 如果存在正常数 $c$ 和 $n_0$，使得当 $n \geq n_0$ 时，$0 \leq f(n) < cg(n)$， 则记为 $f(n) = o(g(n))$。
• 如果存在正常数 $c$ 和 $n_0$，使得当 $n \geq n_0$ 时，$0 \leq cg(n) < f(n)$， 则记为 $f(n) = \omega(g(n))$。

常用函数

取整

• 对任意实数 $x$，$x-1 < \lfloor x \rfloor \leq x \leq \lceil x \rceil < x+1$
• 对任意整数 $n$，$\lceil n/2 \rceil + \lfloor n/2 \rfloor = n$
• 对任意实数 $x \geq 0$ 和整数 $a,b > 0$有 - $\lceil \frac{\lceil x/a \rceil}{b} \rceil = \lceil \frac{x}{ab} \rceil$ - $\lfloor \frac{\lfloor x/a \rfloor}{b} \rfloor = \lfloor \frac{x}{ab} \rfloor$ - $\lceil \frac{a}{b} \rceil \leq \frac{a+(b-1)}{b}$ - $\lfloor \frac{a}{b} \rfloor \geq \frac{a-(b-1)}{b}$

模运算

• $a \pmod n = a - n\lfloor a/n \rfloor$
• $0 \leq a \pmod n < n$

对数

在计算机科学中，认为$lgn = logn = log_2n$

• $a = b^{log_ba}$
• $log_c(ab) = log_ca + log_cb$
• $log_ba^n = n log_ba$
• $log_ba = \frac{log_ca}{log_cb}$
• $log_b(1/a) = -log_ba$
• $log_ba = \frac{1}{log_ab}$
• $a^{log_bc} = c^{log_ba}$

阶乘

详情查看斯特林近似公式

• $n! = o(n^n)$
• $n! = \omega(2^n)$

主定理

主定理的证明请看《算法导论》第三版的 4.6 节。

令 $a \geq 1$ 和 $b > 1$是常数，$f(n)$ 是一个函数，$T(n)$ 是定义在非负整数上的递归式：

$T(n) = aT(n/b) + f(n)$
其中我们将 $n/b$ 解释为 $\lfloor n/b \rfloor$ 或 $\lceil n/b \rceil$。那么 $T(n)$ 有如下渐近界：

1. 若对某个常数 $\epsilon > 0$ 有 $f(n) = O(n^{log_ba-\epsilon})$，则 $T(n)=\Theta(n^{log_ba})$
2. 若 $f(n) = \Theta(n^{log_ba})$，则 $T(n) = \Theta(n^{log_ba}lgn)$
3. 若对某个常数 $\epsilon > 0$ 有 $f(n) = \Omega(n^{log_ba+\epsilon})$，且对某个常数 $c < 1$ 和所有足够大的 $n$ 有 $af(n/b) \leq cf(n)$，则 $T(n) = \Theta(f(n))$

对于三种情况的每一种，我们将函数 $f(n)$ 与函数 $n^{log_ba}$ 进行比较。直觉上，两个函数较大者决定了递归式的解。

• 若函数 $n^{log_ba}$ 更大，如情况 1，则解为 $T(n)=\Theta(n^{log_ba})$。
• 若两个函数大小相当，如情况 2，则乘上一个对数因子，解为 $T(n) = \Theta(n^{log_ba}lgn) = \Theta(f(n)lgn) $
• 若函数 $f(n)$ 更大，如情况 3，则解为 $T(n) = \Theta(f(n))$。

在此直觉之外，我们需要了解一些技术细节。在第一种情况中，不是 $f(n)$ 小于 $n^{log_ba}$ 就够了，而是要多项式意义上的小于。也就是说，$f(n)$ 必须渐近小于 $n^{log_ba}$，要相差一个因子 $n^{\epsilon}$。在第三种情况中，不是 $f(n)$ 大于 $n^{log_ba}$ 就够了，而是要多项式意义上的大于，而且还要满足条件 $af(n/b) \leq cf(n)$。

注意，这三种情况并未覆盖 $f(n)$ 的所有可能性。情况 1 和情况 2 之间有一定的间隙，情况 2 和情况 3 之间也有一定间隙。这样的情况下就不能使用主定理来求解递归式了。