拓扑排序
拓扑排序是对有向无圈图的顶点的一种排序,使得如果存在一条从 $v_i$ 到 $v_j$ 的路径,那么在排序中 $v_j$ 就在 $v_i$ 的之后出现。它的原理比较简单,直接用下面的图片进行展示了。图片来源与拓扑排序(Topological Sorting)
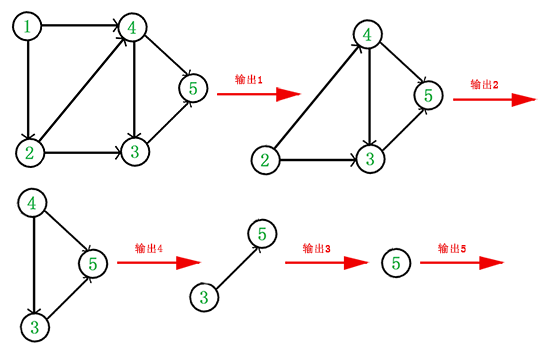
拓扑排序的结果不是唯一的。
最短路径问题
- 对于一个有向附权图,它的边$(vi, v_j)$上的权是$c{i, j+1}$,因此,一条路径$v1v_2…v_n$的值为$\sum{i=1}^{n-1}c_{i,j+1}$,叫作赋权路径长。而无权路径长只是路径上的边数,即 n-1。
- 单源最短路径问题:给定一个有向附权图 G 和一个特定的顶点 s 作为输入,找出从 s 到 G 中每一个其他顶点的最短赋权路径。
- 单源最短路径问题的解可能不唯一。
- 负值圈:如果存在圈,且圈上存在某个边的权值为负数,则称这个圈为负值圈。
- 求解单源最短路径问题时,需要分情况进行讨论,分别是: 1. 无权或者权值均为非负。 2. 无负值圈但有负权。 3. 存在负值圈。这种情况下,在求解最短路径过程中会陷入无限循环,即不存在最短路径。
Dijkstra 算法
在这里,我们介绍 Dijkstra 算法,用它来求解情况 1 下的最短路径。首先,用一张我在网上发现的图片展示 Dijkstra 算法的原理。图片来源轻松搞懂 dijkstra 算法+堆优化 || 原理+实战

Dijkstra 算法实现步骤:
- 对于每一个顶点,有 3 条必要信息:
distance:代表从开始顶点 s 到当前顶点的最短距离。s 的distance = 0,其他顶点在初始时distance为无穷大。path:与distance对应的路径上的前一个顶点。known:该值为true时表示当前顶点的distance值已经是最小的,后续不会再进行更新。初始时,包括 s 在内的所有顶点known = false。
- 从 s 开始遍历每个
known = false的顶点,将当前顶点的known标识为true。找出当前顶点可以邻接到的其他顶点,然后依次根据情况决定是否更新这些被邻接到的顶点的distance和path。最后在所有known = false的顶点中找出distance最小的一个,让它成为下一个当前顶点。 - 当所有顶点的
known均为true时,算法运行结束。
如果有向图是无圈的,则可以改进 Dijkstra 算法原有的顶点选择方式,按照拓扑排序的顺序选择顶点。
如果想要 Dijkstra 算法可以正常工作,必须保证有向图中没有负的权值,否则known将失去存在的意义。
无负值圈但有负权
有的人想到在这种情况下给每个边上的权值都加上一个相同的常数,从而消除负权值,再使用 Dijkstra 算法进行计算。这样做是行不通的,因为这样做会导致边数多的路径相对于边数少的路径,权重更重了。
这种情况的新算法步骤如下所示:
- 每个顶点都有
distance和path属性。同时算法还需要维护一个队列,它里面保存的是需要被遍历的顶点。 - 将开始顶点 s 加入队列中。
- 取出队列中的第一个顶点,找到所有可以被它邻接到的其他顶点,然后依次根据情况决定是否更新这些被邻接到的顶点的
distance和path。 - 在进行步骤 3 时,如果决定更新某个顶点的
distance和path,并且这个被更新的顶点不在队列之中,那么就在更新的同时,将它加入到队列中。 - 重复步骤 3 和步骤 4,直到队列为空。
这个算法的重点在于加顶点加入队列的判断机制。
网络流问题
设给定有向图 G,其任意边$(vi, v_j)$上的容量为$c{i,j}$。这里有两个顶点,一个是发点 s,一个是收点 t。在既不是发点 s 又不是收点 t 的任意顶点 v,总的进入流必须等于总的发出流。最大流问题就是确定从 s 到 t 可以通过的最大流量。例如,下图展示了一个有向图和它的最大流。
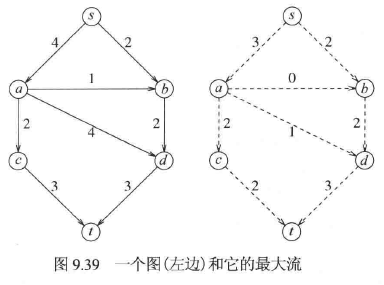
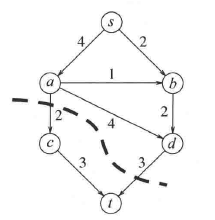
从图中看到,顶点 s 有容量为 4 和 2 的两条边流出,而顶点 t 有容量为 3 和 3 的两条边进入。因此,最大流也许可能是 6 而不是 5。然而,下图指出如何证明最大流就是 5。我们把图切割成两部分:一部分包含顶点 s,而另一部分包含顶点 t。既然流必须通过切口,于是切口上所有的边的总容量就是最大流的一个界。从图中恰好可以看到,5 就是最大流的一个界。
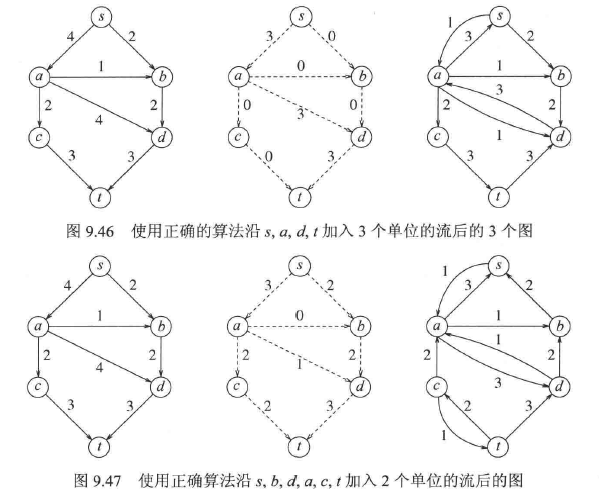
求解最大流问题的首要想法是分阶段进行。我们从图 G 开始并构造一个流图(flow graph)$G_f$。$G_f$表示在求解的任意阶段已经达到的流。开始时$G_f$的所有的边都是没有流的,我们希望当算法终止时$G_f$包含最大流。另外,我们还构造一个图$G_r$,称为残余图(residual graph),它表示对于每条边还能再添加上多少流。对于每一条边,可以从容量中减去当前的流而计算除残余的流。$G_r$的边叫作残余边(residual edge)。在每个阶段,我们寻找图$G_r$中从 s 到 t 的一条路径,这条路径叫作增长通路(augmenting path)。这条路径上的最小容量就是可以添加到路径每一边上的流的量。下面用一个图展示这些概念。
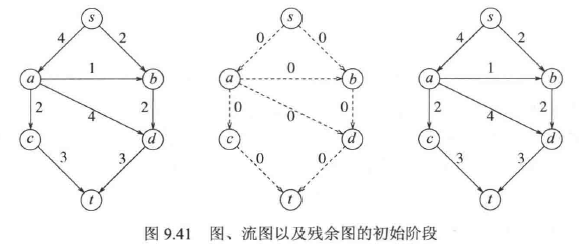
下面给出求解最大流问题的具体步骤:
- 在$G_r$中找到任意一条增长通路,根据该增长通路,更新$G_f$中的的流信息,然后在$G_r$将该增长路径调整为相反方向。
- 重复步骤 1,直到在$G_r$中找不到增长通路位置。
其实步骤 1 中的增长通路的选择上可以做一些文章从而减少时间复杂度,这里暂时不进行详细分析了。