树

发表于 | 更新于 | 分类于

树的基本概念

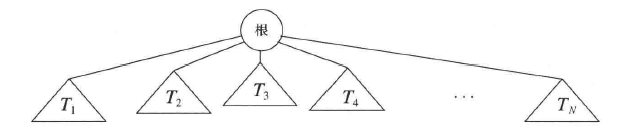
一棵树是一些节点的集合，这个集合可以是空集；若不是空集，则树由称做根（root）的节点$r$及 0 或多个非空的（子）树$T_1,T_2, ···,T_k$组成，这些子树中每一颗的根都被来自根$r$的一条有向的边所连接。每一颗子树的根叫作根$r$的儿子，而$r$是每一颗子树的根的父亲

一般的树

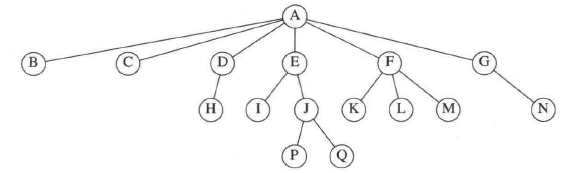
下图中，节点 A 是根。节点 F 有一个父亲 A 并且有儿子 K、L 和 M。每一个节点可以有任意多个儿子，也可能是零个儿子。没有儿子的节点称为树叶，下图中的树叶是 B、C、H、I、P、Q、K、L、M 和 N。具有相同父亲的节点为兄弟。因此，K、L 和 M 都是兄弟。

一颗树

从节点$n_1$到$n_k$的路径定义为节点$n_1, n_2, ···, n_k$的一个序列，使得对于$1 \leq i \leq k$的节点$n_i$是$n$$i+1$的父亲。这条路径的长是该路径上边的条数，即$k - 1$。从每一个节点到它自己有一条长为 0 的路径。注意，在一棵树中从根到每个节点恰好存在一条路径

对任意节点$n_i$，$n_i$的深度为从根到$n_i$的唯一路径的长。因此，根的深度为 0。节点$n_i$的高是从$n_i$到一片树叶的最长路径的长。因此所有树叶的高都是 0。一棵树的高等于它的根的高。上图中的树，E 的深度为 1 而高为 2；F 的深度为 1 而高也是 1；该树的高为 3。一棵树的深度等于其最深的树叶的深度，该深度总是等于这棵树的高

二叉树

二叉树的种类

  • 二叉树：是一种特殊的树，它每个节点最多只能有两个儿子
  • 完美二叉树：高为 h，且节点数为$2^{h+1} - 1$的二叉树。也就是说除了最后一层无任何子节点之外，每一层上的所有节点都有两个儿子
  • 完全二叉树：从根节点到倒数第二层满足完美二叉树，最后一层没有完全填满，其叶子节点都靠左对齐。一颗高为 h 的完全二叉树有$2^h$到$2^{h+1} - 1$个节点。这意味着，完全二叉树的高是$\lfloor logN \rfloor$，显然它是$O(logN)$
  • 完满二叉树：对于任意节点，要不就是拥有两个儿子，要不就是一个儿子都没有
  • 堆：特殊的完全二叉树，后续文章会详细介绍
  • 二叉查找树：使二叉树成为二叉查找树的性质是，对于树中的每个节点 X，它的左子树中所有项的值均小于 X 中的项，而它的右子树中所有项的值均大于 X 中的项
  • AVL 树：带有平衡条件的二叉查找树

二叉树的遍历

  • 先序遍历：首先处理根节点，然后再处理它的左儿子和右儿子
  • 中序遍历：首先处理左儿子，然后处理根节点，最后处理右儿子
  • 后序遍历：首先处理左儿子，然后处理右儿子，最后处理根节点
  • 层序遍历：按照从上到下、从左到右的顺序处理节点

先序遍历

递归

1
2
3
4
5
6
7
8
function preOrderTraverse(node) {
  if (node) {
    console.log(node.val);

    preOrderTraverse(node.left);
    preOrderTraverse(node.right);
  }
}

非递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function preOrderTraverse(node) {
  const stack = [];
  let cur = node;

  while (cur || stack.length > 0) {
    while (cur) {
      console.log(cur.val);

      stack.push(cur);
      cur = cur.left;
    }

    if (stack.length > 0) {
      cur = stack.pop().right;
    }
  }
}

中序遍历

递归

1
2
3
4
5
6
7
8
9
function middleOrderTraverse(node) {
  if (node) {
    middleOrderTraverse(node.left);

    console.log(node.val);

    middleOrderTraverse(node.right);
  }
}

非递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function middleOrderTraverse(node) {
  const stack = [];
  let cur = node;

  while (cur || stack.length > 0) {
    while (cur) {
      stack.push(cur);
      cur = cur.left;
    }

    if (stack.length > 0) {
      const topNode = stack.pop();
      console.log(topNode.val);
      cur = topNode.right;
    }
  }
}

后序遍历

递归

1
2
3
4
5
6
7
8
function postOrderTraverse(node) {
  if (node) {
    postOrderTraverse(node.left);
    postOrderTraverse(node.right);

    console.log(node.val);
  }
}

非递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function postOrderTraverse(node) {
  const stack = [];

  let cur = node;
  let lastHandled = null;

  while (cur || stack.length > 0) {
    while (cur) {
      stack.push(cur);
      cur = cur.left;
    }

    if (stack.length > 0) {
      const topNode = stack[stack.length - 1];

      if (topNode.right && topNode.right !== lastHandled) {
        cur = topNode.right;
      } else {
        console.log(topNode.val);
        lastHandled = topNode;
        stack.pop();
      }
    }
  }
}

层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function levelOrderTraverse(node) {
  if (!node) {
    return;
  }

  const queue = [node];

  while (queue.length > 0) {
    const prevLevelNode = queue.shift();
    console.log(prevLevelNode.value);

    if (prevLevelNode.left) {
      queue.push(prevLevelNode.left);
    }

    if (prevLevelNode.right) {
      queue.push(prevLevelNode.right);
    }
  }
}

二叉查找树

二叉查找树与普通的二叉树相比，有如下特点：

  • 所有节点彼此互异，即不存在相同的节点
  • 对于树中的任意节点 X，它的左子树中所有项的值均小于 X 中的项，而它的右子树中所有项的值均大于 X 中的项

下面是实现一个二叉查找树的代码：

从二叉查找树中移除元素是这部分的难点，首先定位到要移除元素所在节点，然后进行如下 3 种操作：

  1. 如果当前节点为树叶，那么直接删除该树叶
  2. 如果当前节点拥有一个子树，那么用该子树的根节点替换当前节点
  3. 如果当前节点拥有两个子树，那么找出右子树中的最小节点并递归的删除该最小节点，然后将这个最小节点的值赋给当前节点的值（也可以采用相反的方式，去寻找左子树中的最大节点）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
class BinarySearchTree {
  constructor(newValue) {
    this.value = newValue;
    this.left = null;
    this.right = null;
    this.isNode = true;
  }

  static makeTree(array) {
    let tree = new BinarySearchTree(array[0]);
    array.slice(1).forEach((item) => {
      tree.insert(item);
    });
    return tree;
  }

  insert(newNode, currentNode = this) {
    if (!newNode.isNode) {
      newNode = new BinarySearchTree(newNode);
    }

    if (newNode.value < currentNode.value) {
      if (currentNode.left) {
        currentNode.insert(newNode, currentNode.left);
      } else {
        currentNode.left = newNode;
      }
    }

    if (newNode.value > currentNode.value) {
      if (currentNode.right) {
        currentNode.insert(newNode, currentNode.right);
      } else {
        currentNode.right = newNode;
      }
    }

    if (newNode.value === currentNode.value) {
      console.log(`${newNode.value} already exists`);
    }
  }

  contains(inputValue, currentNode = this) {
    if (inputValue < currentNode.value) {
      if (currentNode.left) {
        return currentNode.contains(inputValue, currentNode.left);
      } else {
        return false;
      }
    }

    if (inputValue > currentNode.value) {
      if (currentNode.right) {
        return currentNode.contains(inputValue, currentNode.right);
      } else {
        return false;
      }
    }

    if (inputValue === currentNode.value) {
      return true;
    }
  }

  findMin(currentNode = this) {
    if (currentNode.left) {
      return currentNode.findMin(currentNode.left);
    } else {
      return currentNode.value;
    }
  }

  findMax(currentNode = this) {
    if (currentNode.right) {
      return currentNode.findMin(currentNode.right);
    } else {
      return currentNode.value;
    }
  }

  // preNode和where参数完全是为了删除树叶准备的
  remove(inputValue, currentNode = this, preNode = null, where = '') {
    if (inputValue < currentNode.value) {
      if (currentNode.left) {
        currentNode.remove(inputValue, currentNode.left, currentNode, 'left');
      } else {
        console.log(`${inputValue} does not exist`);
      }
    }

    if (inputValue > currentNode.value) {
      if (currentNode.right) {
        currentNode.remove(inputValue, currentNode.right, currentNode, 'right');
      } else {
        console.log(`${inputValue} does not exist`);
      }
    }

    if (inputValue === currentNode.value) {
      if (!currentNode.left && !currentNode.right) {
        preNode[where] = null;
        return;
      }

      if (!currentNode.left) {
        currentNode = currentNode.right;
        return;
      } else if (!currentNode.right) {
        currentNode = currentNode.left;
        return;
      }

      if (currentNode.left && currentNode.right) {
        let minValue = currentNode.right.findMin();
        currentNode.remove(minValue, currentNode.right, currentNode, 'right');
        currentNode.value = minValue;
        return;
      }
    }
  }
}

let array = [6, 2, 8, 7, 1, 4, 3, 5],
  tree = BinarySearchTree.makeTree(array);

function preOrderTraverse(node, result = '') {
  result += node.value + '  ';

  if (node.left) {
    result = preOrderTraverse(node.left, result);
  }

  if (node.right) {
    result = preOrderTraverse(node.right, result);
  }

  return result;
}

console.log(preOrderTraverse(tree)); // 6  2  1  4  3  5  8  7

tree.remove(4);
console.log(preOrderTraverse(tree)); // 6  2  1  5  3  8  7

tree.insert(4);
console.log(preOrderTraverse(tree)); // 6  2  1  5  3  4  8  7

tree.remove(41); // 41 does not exist
console.log(preOrderTraverse(tree)); // 6  2  1  5  3  4  8  7

AVL 树

基本概念

  • AVL 树是带有平衡条件的二叉查找树
  • 平衡条件为每个节点的左子树和右子树的高度最多差 1（空树的高度定义为-1）

如果要对一个 AVL 树进行插入操作，需要更新通向根节点路径上那些节点的所有平衡信息，而插入操作隐含着困难的原因在于，插入一个节点可能破坏 AVL 树的平衡特性。如果发生这种情况，那么可以通过旋转来恢复 AVL 树的平衡

在一次插入之后，从插入点到根节点的路径上寻找其中深度最深（或高度最小）的不平衡节点，称该节点为 A，造成不平衡的插入分为下面四种情况：

  1. 对 A 的左儿子的左子树进行一次插入
  2. 对 A 的左儿子的右子树进行一次插入
  3. 对 A 的右儿子的左子树进行一次插入
  4. 对 A 的右儿子的右子树进行一次插入

删除操作会出现的情况与插入类似，不单独介绍了。

情况 1 和情况 4 是关于 A 点的镜像对称，使用单旋转来处理，原理如下图所示

AVL1
AVL4

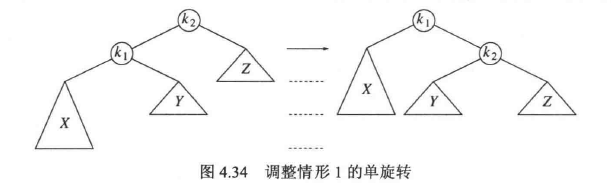
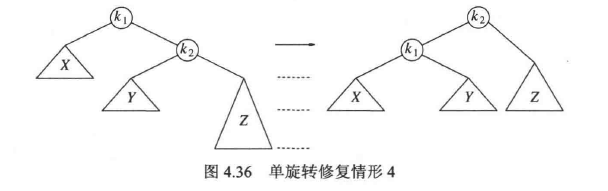
情况 2 和情况 3 也是关于点的镜像对称，使用双旋转来处理，原理如下图所示，因为子树 B 和 C 中有一颗比 D 深两层，但是我们不能肯定是哪一颗，所以图中 B 和 C 都被画成比 D 低 1.5 层

AVL2
AVL3

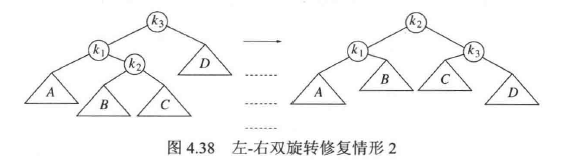
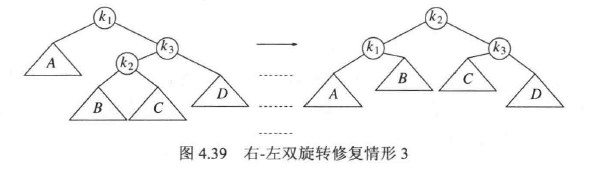
实现

我实现二叉查找树和 AVL 树的代码书写思路不同，最主要的区别是插入和删除操作是否有返回值。普通二叉树没有利用返回值，而 AVL 树的插入和删除操作都会返回新的 AVL 树 🌲！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
class AVLTree {
  constructor(newValue) {
    this.value = newValue;
    this.left = null;
    this.right = null;
    this.height = 0;
    this.isNode = true;
  }

  static makeTree(array) {
    let tree = new AVLTree(array[0]);
    array.slice(1).forEach((item) => {
      tree = tree.insert(item);
    });
    return tree;
  }

  insert(newNode, currentNode = this) {
    if (!newNode.isNode) {
      newNode = new AVLTree(newNode);
    }

    if (newNode.value < currentNode.value) {
      if (currentNode.left) {
        currentNode.left = currentNode.insert(newNode, currentNode.left);
      } else {
        currentNode.left = newNode;
      }
    }

    if (newNode.value > currentNode.value) {
      if (currentNode.right) {
        currentNode.right = currentNode.insert(newNode, currentNode.right);
      } else {
        currentNode.right = newNode;
      }
    }

    if (newNode.value === currentNode.value) {
      console.log(`${newNode.value} already exists`);
    }

    currentNode = currentNode.balanceTree(currentNode);

    return currentNode;
  }

  // 只要树的结构发生改变就要触发这个函数
  // 负责保持树的平衡和更新节点的高度信息
  balanceTree(currentNode) {
    function getTreeHeight(currentNode) {
      if (!currentNode) {
        return -1;
      } else {
        return currentNode.height;
      }
    }

    function rotateWithLeftChild(currentNode) {
      let nextNode = currentNode.left;

      currentNode.left = nextNode.right;
      nextNode.right = currentNode;

      return nextNode;
    }

    function rotateWithRightChild(currentNode) {
      let nextNode = currentNode.right;

      currentNode.right = nextNode.left;
      nextNode.left = currentNode;

      return nextNode;
    }

    function doubleWithLeftChild(currentNode) {
      currentNode.left = rotateWithRightChild(currentNode.left);
      currentNode = rotateWithLeftChild(currentNode);
      return currentNode;
    }

    function doubleWithRightChild(currentNode) {
      currentNode.right = rotateWithLeftChild(currentNode.right);
      currentNode = rotateWithRightChild(currentNode);
      return currentNode;
    }

    if (
      getTreeHeight(currentNode.left) - getTreeHeight(currentNode.right) >
      1
    ) {
      if (
        getTreeHeight(currentNode.left.left) >=
        getTreeHeight(currentNode.left.right)
      ) {
        currentNode = rotateWithLeftChild(currentNode);
      } else {
        currentNode = doubleWithLeftChild(currentNode);
      }
    }

    if (
      getTreeHeight(currentNode.right) - getTreeHeight(currentNode.left) >
      1
    ) {
      if (
        getTreeHeight(currentNode.right.right) >=
        getTreeHeight(currentNode.right.left)
      ) {
        currentNode = rotateWithRightChild(currentNode);
      } else {
        currentNode = doubleWithRightChild(currentNode);
      }
    }

    function updateHeight(currentNode) {
      currentNode.height =
        Math.max(
          getTreeHeight(currentNode.left),
          getTreeHeight(currentNode.right)
        ) + 1;
    }

    if (currentNode.left) {
      updateHeight(currentNode.left);
    }

    if (currentNode.right) {
      updateHeight(currentNode.right);
    }

    updateHeight(currentNode);

    return currentNode;
  }

  remove(inputValue, currentNode = this) {
    if (inputValue < currentNode.value) {
      if (currentNode.left) {
        currentNode.left = currentNode.remove(
          inputValue,
          currentNode.left,
          currentNode,
          'left'
        );
      } else {
        console.log(`${inputValue} does not exist`);
      }
    }

    if (inputValue > currentNode.value) {
      if (currentNode.right) {
        currentNode.right = currentNode.remove(
          inputValue,
          currentNode.right,
          currentNode,
          'right'
        );
      } else {
        console.log(`${inputValue} does not exist`);
      }
    }

    if (inputValue === currentNode.value) {
      switch (true) {
        case !currentNode.left && !currentNode.right:
          currentNode = null;
          break;

        case !currentNode.left:
          currentNode = currentNode.right;
          break;

        case !currentNode.right:
          currentNode = currentNode.left;
          break;

        case currentNode.left && currentNode.right:
          let minValue = currentNode.right.findMin();
          currentNode = currentNode.remove(
            minValue,
            currentNode.right,
            currentNode,
            'right'
          );
          currentNode.value = minValue;
          break;

        default:
          break;
      }
    }

    if (currentNode) {
      currentNode = currentNode.balanceTree(currentNode);
    }

    return currentNode;
  }
}

function preOrderTraverse(node, result = '') {
  result += node.value + '  ';

  if (node.left) {
    result = preOrderTraverse(node.left, result);
  }

  if (node.right) {
    result = preOrderTraverse(node.right, result);
  }

  return result;
}

let array = [1, 2, 3, 4, 5, 6, 7, 16, 15],
  tree = AVLTree.makeTree(array);

console.log(preOrderTraverse(tree)); // 4  2  1  3  6  5  15  7  16

tree = tree.insert(14);
console.log(preOrderTraverse(tree)); // 4  2  1  3  7  6  5  15  14  16

tree = tree.remove(6);
console.log(preOrderTraverse(tree)); // 4  2  1  3  7  5  15  14  16

tree = tree.remove(5);
console.log(preOrderTraverse(tree)); // 4  2  1  3  15  7  14  16

树的遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
function traverseTree(root) {
  const stack = [];
  let cur = root;

  while (cur || stack.length > 0) {
    while (cur) {
      // preOrderTraverse

      stack.push(cur);

      cur.visitedIndex = -1;

      if (cur.children.length > 0) {
        cur.visitedIndex += 1;
        cur = cur.children[cur.visitedIndex];
      } else {
        cur = null;
      }
    }

    if (stack.length > 0) {
      const topNode = stack[stack.length - 1];

      if (topNode.children.length - 1 > topNode.visitedIndex!) {
        topNode.visitedIndex! += 1;
        cur = topNode.children[topNode.visitedIndex!];
      } else {
        // postOrderTraverse

        stack.pop();
        delete topNode.visitedIndex;
        cur = null;
      }
    }
  }
}

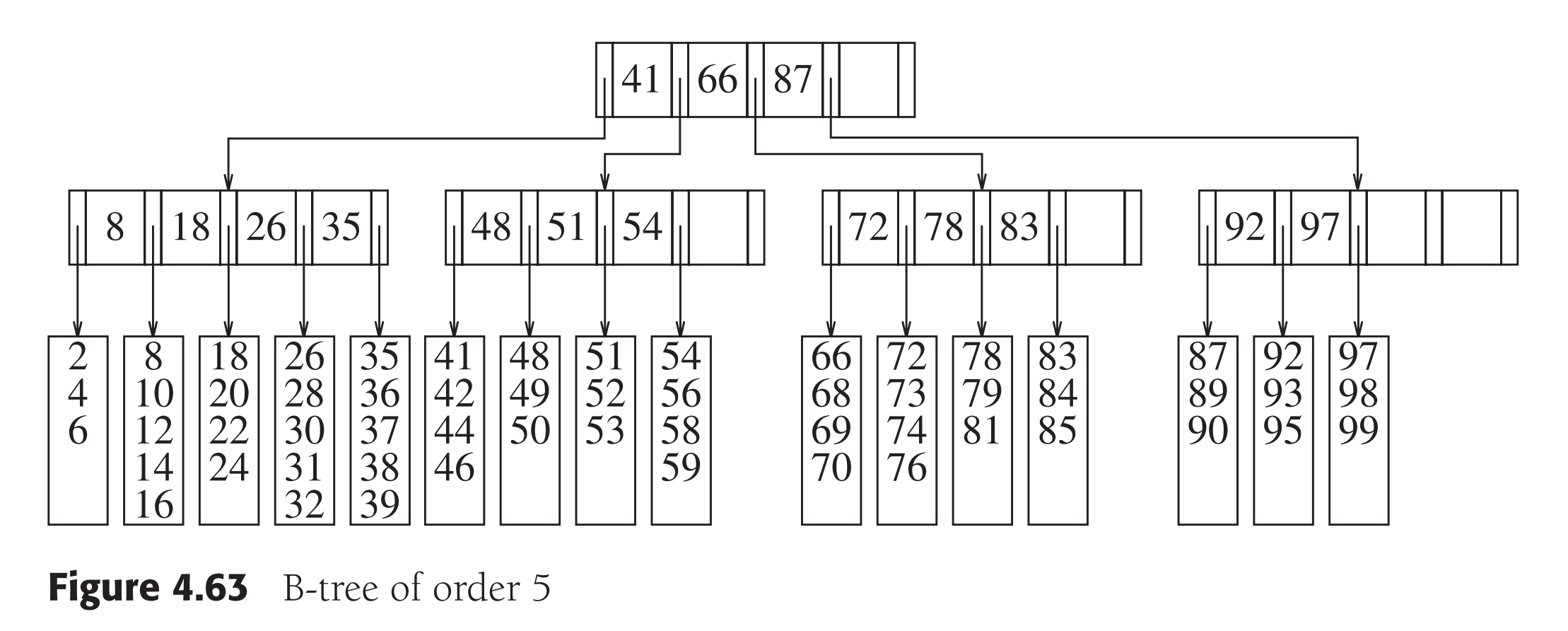
B 树

阶为 $M$ 的 B 树是一颗具有下列特性的 $M$ 叉树：

  1. 数据全部存储在叶节点上；
  2. 非叶节点最多可以存储 $M-1$ 个关键字，以指示搜索的方向。关键字 $i$ 代表子树 $i+1$ 中最小的关键字；
  3. 树的根如果有子节点，则子节点个数一定在 2 和 $M$ 之间；
  4. 除根外，所有非叶节点的子节点个数在 $\lceil M/2 \rceil$ 和 $M$ 之间；
  5. 所有树叶的深度相同，并且每片树叶上存储的数据个数在 $\lceil L/2 \rceil$ 和 $L$ 之间。$L = 节点可容纳数据个数 = 节点容量/数据大小$

B-Tree Demo



感谢您的阅读，如果发现文章中有错误或漏洞，请批评指正。
邮箱：aadonkeyz@gmail.com

0%