基本概念
散列表是一种用于以常数平均时间执行插入、删除和查找的技术。但是,那些需要元素间任何序信息的树操作在这里将不会得到有效的支持(如findMin、findMax)。理想的散列表只不过是一个具有固定大小的数组。假定散列表长度为n,当向散列表中插入数据时,将该数据的关键字(key)作为输入传递给一个称作散列函数(hash function)的映射函数,然后得到一个 0 ~ n-1 的数值,这个数值代表的是该数据插入散列表的位置。给定两个不同的关键字,如果散列函数的输出结果相同,这种情况叫作冲突(collision)。
如果输入的关键字是整数,则一般合理的方法是直接返回 Key mod TableSize,除非 Key 碰巧具有某些不理想的性质。例如,若表的大小是 10 而关键字都以 0 为个位,则此时上述标准的散列函数就是一个坏的选择。为了避免这样的情况,通常保证表的大小是素数,当输入的关键字是随机整数时,散列函数不仅计算起来非常简单,而且关键字的分配也很均匀,减少了冲突的发生。
分离链表法
解决冲突的第一种方法叫作分离链表法,其做法是将散列到同一个值的所有元素保留到一个链表中。
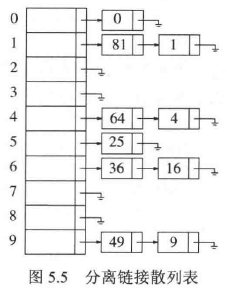
为了执行一次 search,需要使用散列函数来确定究竟遍历哪个链表,然后在适当的链表中执行一次查找。为执行 insert,需要检查相应的链表看看该元素是否已经处在相应的位置。如果这个元素是个新的元素,那么它将被插入到链表的前端,这不仅是因为方便,而且还因为常常发生这样的事实:新近插入的元素最有可能不久又被访问。
除链表外,任何合理的方案也都可以解决冲突现象,一颗二叉查找树或甚至另一个散列表都将胜任这个工作,但是我们期望,如果散列表是大的并且散列函数是好的,那么所有的链表都应该是短的,从而基本的分离链表法就没有必要再尝试任何复杂的手段了。
我们定义散列表的装填因子 λ 为散列表中的元素个数对该表大小的比。在上面的例子中,λ = 1.0。链表的平均长度为 λ。执行一次查找所需的代价,是计算散列函数值所需要的常数时间加上遍历所用的时间。在一次不成功的查找中,要遍历的节点数平均为 λ。一次成功的查找则需要遍历大约 1+(λ/2) 个链。
开放定址法
分离链表法的缺点是使用一些链表,由于给新单元分配地址需要时间,因此这就导致算法的速度有些减慢,同时算法实际上还要求对第二种数据结构的实现。而开放定址法解决冲突的思路是尝试另外一些单元,直到找出空的单元为止。一般来说,对于使用开放定址法的散列表,其装填因子应该满足λ < 0.5。
线性探测法
当发生冲突时,从当前位置开始,依次往后进行探测,当探测到空闲位置时,插入元素。
下面例子中,$hash(x) = x mod n, n = 10$,插入项:{89, 18, 49, 58, 69}。
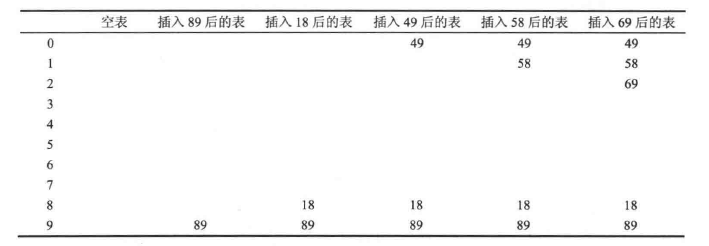
只要表足够大,使用线性探测法总能够找到一个空闲为止,但是如此花费的时间是相当多的。更糟的是,即使表相对较空,这样占据的为止也会开始形成一些区块,其结果称为一次聚焦,就是说,散列到区块中的任何数据都需要多次试选单元才能够解决冲突,然后该数据被添加到相应的区块中。
平方探测法
当发生冲突时,从当前位置开始,依次探测当前位置之后的第 $1, 2^2, 3^2, 4^2, …$ 个位置,当探测到空闲位置时,插入元素。
下面例子中,$hash(x) = x mod n, n = 10$,插入项:{89, 18, 49, 58, 69}。
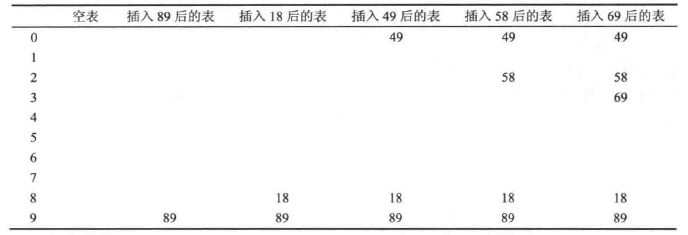
使用平方探测时,如果表的大小是素数,同时表至少还有一半的空余位置,那么新的元素一定可以探测到空余位置。
对于线性探测,让散列表几乎填满元素并不是个好主意,因为此时表的性能会降低。对于平方探测情况甚至更糟,一旦表被填满超过一半,或者表的长度不是素数,就不能保证可以探测到空余位置了。这是因为可以用作解决冲突的备选位置最多只有表长度的一半。
虽然平方探测排除了一次聚焦,但是散列到同一位置上的那些元素将探测相同的备选单元。这叫作二次聚焦。二次聚焦是理论上的一个小缺憾。
双散列
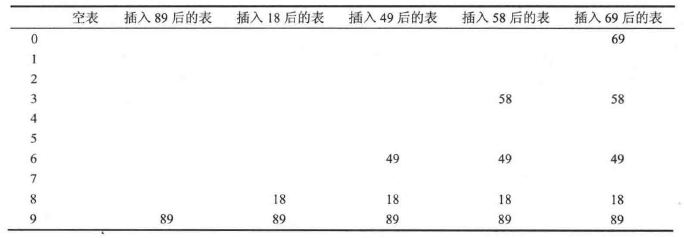
当发生冲突时,使用第二个散列函数计算 $d=hash_2(x)$,然后依次探测当前位置之后的第 $d, 2d, 3d, …$ 个位置,当探测到空闲位置时,插入元素。
下面例子中,$hash_1(x) = x mod n, hash_2(x) = 7 - (x mod 7), n = 10$,插入项:{89, 18, 49, 58, 69}。
再散列
再散列是为了解决插入操作运行时间过长的问题,而不是为了解决冲突。
对于使用平方探测的开放定址散列法,如果散列填的太满,那么操作的运行时间将消耗过长,且插入操作可能失败。这可能发生在有太多的删除和插入混杂的场合。此时,一种解决方法是建立另外一个大约两倍大的表(而且使用一个相关的新散列函数),扫描整个原始散列表,计算每个(未删除的)元素的新散列值并将其插入到新表中。
下面用一个例子演示再散列的过程。


